Advertencia¶

Parte I¶

El origen de la Mecánica Cuántica¶

Episodio I : Old quantum mechanics¶

In [2]:
utils.IFrame(src='https://phet.colorado.edu/sims/html/wave-interference/latest/wave-interference_en.html',
       width='600px',
    height='400px')
Out[2]:

Radiación del Cuerpo Negro y cuantización de la energía¶

In [3]:
utils.Photo('Wien')
Out[3]:
No description has been provided for this image

$${\displaystyle B_{\nu }(T)\approx {\frac {2h\nu ^{3}}{c^{2}}}e^{-{\frac {h\nu }{k_{\mathrm {B} }T}}}}$$

In [4]:
utils.Photo('Plank')
Out[4]:
No description has been provided for this image

$${\displaystyle B_{\nu }(\nu ,T)={\frac {2h\nu ^{3}}{c^{2}}}{\frac {1}{e^{\frac {h\nu }{k_{\mathrm {B} }T}}-1}}}$$

$${\displaystyle B_{\nu }(T)={\frac {2\nu ^{2}k_{\mathrm {B} }T}{c^{2}}}}$$

In [5]:
utils.IFrame(src='https://phet.colorado.edu/sims/html/blackbody-spectrum/latest/blackbody-spectrum_en.html',
       width='600px',
    height='400px')
Out[5]:

Efecto Fotoeléctrico¶

In [6]:
utils.Photo('Einstein')
Out[6]:
No description has been provided for this image

Simulación interactiva

In [7]:
utils.Photo('Rutherford')
Out[7]:
No description has been provided for this image
In [8]:
utils.IFrame(src='https://phet.colorado.edu/sims/html/rutherford-scattering/latest/rutherford-scattering_en.html',
       width='600px',
       height='400px')
Out[8]:

Espectro Atómico (Bohr, DeBroglie, Sommerfeld, Kramer)¶

In [9]:
utils.Photo('Bohr')
Out[9]:
No description has been provided for this image
In [10]:
utils.Photo('de Broglie')
Out[10]:
No description has been provided for this image

$$ E=n\hbar \omega \, $$ $$ \int p\,dx=\hbar \int k\,dx=2\pi \hbar n $$

In [11]:
utils.Photo('Sommerfeld')
Out[11]:
No description has been provided for this image

$$ \oint \limits _{H(p,q)=E}p_{i}\,dq_{i}=n_{i}h $$

In [12]:
utils.Photo('Kramers')
Out[12]:
No description has been provided for this image

$$ X_{n}(t)=\sum _{k=-\infty }^{\infty }e^{ik\omega t}X_{n;k} $$

Momento angular de los electrones / Spin (Stern-Gerlach)¶

In [13]:
utils.Photo('Stern')
Out[13]:
No description has been provided for this image
In [14]:
utils.Photo('Gerlach')
Out[14]:
No description has been provided for this image

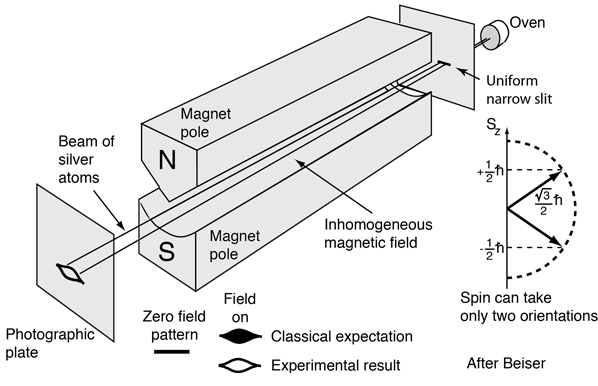
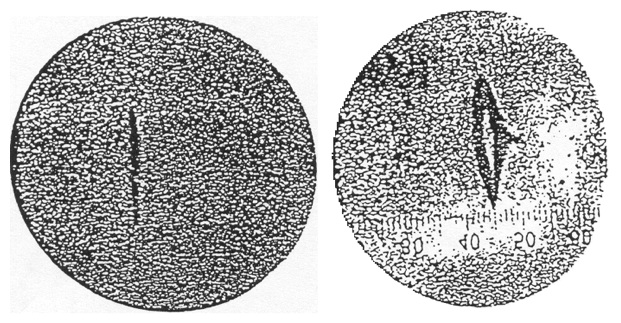
Simulación y comparación del modelo clásico y cuántico del momento mágnetico de un átomo¶

https://nbviewer.jupyter.org/github/qutip/qutip-notebooks/blob/master/examples/stern-gerlach-tutorial.ipynb

Episodio II¶

Modelos matemáticos de la MC¶

In [15]:
utils.Photo('Heisenberg')
Out[15]:
No description has been provided for this image

Mecánica matricial de Heisenberg¶

$$X_{{nm}}(t)=e^{{2\pi i(E_{n}-E_{m})t/h}}X_{{nm}}(0)$$

$$ {\sqrt {2}}X(0)={\sqrt {{\frac {h}{2\pi }}}}\;{\begin{bmatrix}0&{\sqrt {1}}&0&0&0&\cdots \\{\sqrt {1}}&0&{\sqrt {2}}&0&0&\cdots \\0&{\sqrt {2}}&0&{\sqrt {3}}&0&\cdots \\0&0&{\sqrt {3}}&0&{\sqrt {4}}&\cdots \\\vdots &\vdots &\vdots &\vdots &\vdots &\ddots \\\end{bmatrix}} $$

In [16]:
utils.Photo('Born')
Out[16]:
No description has been provided for this image
In [17]:
utils.Photo('Jordan')
Out[17]:
No description has been provided for this image

$$ (XP)_{{mn}}=\sum _{{k=0}}^{\infty }X_{{mk}}P_{{kn}} $$

$$ \sum _{k}(X_{{nk}}P_{{km}}-P_{{nk}}X_{{km}})={ih \over 2\pi }~\delta _{{nm}} $$

$$ \frac{dA}{dt} = {i \over \hbar } [ H , A ] + \frac{\partial A}{\partial t} $$

In [18]:
utils.Photo('Schrodinger')
Out[18]:
No description has been provided for this image

Mecánica ondulatoria de Schrodinger¶

$$i{\partial \over \partial t}\psi _{t}(x)=\left[-{1 \over 2m}{\partial ^{2} \over \partial x^{2}}+V(x)\right]\psi _{t}(x)$$

In [ ]:

Formalización y notación de Bra-Ket¶

In [19]:
utils.Photo('Dirac')
Out[19]:
No description has been provided for this image
In [20]:
utils.Photo('von Neumann')
Out[20]:
No description has been provided for this image

$$ |\psi\rangle $$

$${\displaystyle \Psi (\mathbf {r} )\ {\stackrel {\text{def}}{=}}\ \langle \mathbf {r} |\Psi \rangle }$$

Parte II¶

Introducción a la matemática de la MC¶

A Hilbert space H is a real or complex inner product space that is also a complete metric space with respect to the distance function induced by the inner product

fleabag_what

A little Aaronson time¶

QM = Prob + "-"¶

Probabilidad¶

Sea un conjunto de eventos posibles $\Omega$

$$f(x)\in [0,1]{\mbox{ para todo }}x\in \Omega$$ $$\sum _{x\in \Omega }f(x)=1 $$

In [21]:
from sympy import Matrix, init_printing
init_printing(use_latex=True)
In [22]:
Ma, Mb, Mc = Matrix([[1/2,1/2],[1/2,1/2]]), Matrix([[1/3,1/5],[2/3,4/5]]), Matrix([[99/100,0],[1/100,1]])
s = Matrix([[1],[0]])
Ma*s, Mb*s, Mc*s
Out[22]:
$\displaystyle \left( \left[\begin{matrix}0.5\\0.5\end{matrix}\right], \ \left[\begin{matrix}0.333333333333333\\0.666666666666667\end{matrix}\right], \ \left[\begin{matrix}0.99\\0.01\end{matrix}\right]\right)$
In [23]:
Ma
Out[23]:
$\displaystyle \left[\begin{matrix}0.5 & 0.5\\0.5 & 0.5\end{matrix}\right]$
In [ ]:
In [24]:
Mb**200 * s
Out[24]:
$\displaystyle \left[\begin{matrix}0.230769230769232\\0.769230769230774\end{matrix}\right]$

¿Qué obtendríamos si en vez de la Norma 1 imponemos la condición de normalización con la Norma 2?¶

$$f(x)\in \mathbb {C} {\mbox{ para todo }}x\in \Omega$$ $$\sum _{x\in \Omega }\overline {f(x)}* f(x) =1 $$

In [25]:
from sympy import sqrt, symbols, Symbol, init_printing
from sympy.physics.quantum import Bra, Ket, Dagger, Operator

Postulados de la MC¶

Postulado 1¶

El estado de todo sistema físico está representado por un vector (de norma unidad) en un espacio de Hilbert $\mathcal{H}$

In [26]:
a, b = symbols('alpha beta',complex=True)
psi, phi = Ket('psi'),Ket('phi')

estado = a * psi + b * phi
estado
Out[26]:
$\displaystyle \alpha {\left|\psi\right\rangle } + \beta {\left|\phi\right\rangle }$
In [27]:
Dagger(estado)
Out[27]:
$\displaystyle \overline{\alpha} {\left\langle \psi\right|} + \overline{\beta} {\left\langle \phi\right|}$
In [28]:
( Dagger(estado) * estado ).doit()
Out[28]:
$\displaystyle \left(\overline{\alpha} {\left\langle \psi\right|} + \overline{\beta} {\left\langle \phi\right|}\right) \left(\alpha {\left|\psi\right\rangle } + \beta {\left|\phi\right\rangle }\right)$

Postulado 2¶

Todas las propiedades observables de un sistema físico se prepresentan por un operador lineal hermítico que actúa sobre $\mathcal{H}$

In [ ]:

Postulado 3¶

Los resultados posibles de la medición de cualquier observable $A$ son sus autovalores $a_n$

In [ ]:

Postulado 4 ( Regla de Born )¶

Si el estado de un sistema es $\left|\Psi\right\rangle$, la probabilidad de obtener el resultado $a_n$ en la medición del observable $A$ es siempre

$$ Prob\left(a_n | \left|\Psi\right\rangle \right) = \left\langle \Psi\right| P_n \left|\Psi\right\rangle $$

donde $P_n$ es el proyector asociado al autovalor $a_n$. Si $A$ es no degenerado entonce $P_n = {\left|\phi_{n}\right\rangle }{\left\langle \phi_{n}\right|}$ y la probabilidad resulta ser $$Prob\left( a_n | \left|\Psi\right\rangle \right) = \left| \left\langle \phi_{n} |\Psi\right\rangle \right|^2$$

In [ ]:

Postulado 5 ( Postulado de proyección o colapso )¶

Si el estado de un sistema es ${\left|\Psi\right\rangle }$ y medimos el observable $A$ y detectamos el autovalor $a_n$, entonces el estado del sistema después de la medición es la proyección de ${\left|\Psi\right\rangle }$ sobre el subespacio asociado al autovalor $a_n$

In [ ]:
In [ ]:
In [ ]:
In [ ]:

Parte III¶

Sistemas compuestos¶

In [29]:
from sympy.physics.quantum import TensorProduct
In [30]:
j,k,l = Ket('j'), Ket('k'), Ket('l')
A, B = Operator('A'), Operator('B')
In [31]:
jk = TensorProduct(j,k)
jk
Out[31]:
$\displaystyle {{\left|j\right\rangle }}\otimes {{\left|k\right\rangle }}$

Partículas idénticas¶

Paradoja de EPR¶

$$|\Phi ^{+}\rangle ={\frac {1}{{\sqrt {2}}}}(|0\rangle _{A}\otimes |0\rangle _{B}+|1\rangle _{A}\otimes |1\rangle _{B})$$

In [32]:
from sympy.physics.quantum.qubit import Qubit
In [33]:
( Qubit('00') + Qubit('11') )/sqrt(2)
Out[33]:
$\displaystyle \frac{\sqrt{2} \left({\left|00\right\rangle } + {\left|11\right\rangle }\right)}{2}$

Desigualdad de Bell¶

Ejemplo de Teleportación