Interoperabilidad entre Python y Julia Lang

saxa.xyz/charla-cata

@sashakile

https://saxa.xyz/charla-cata

Demo de la Simulación

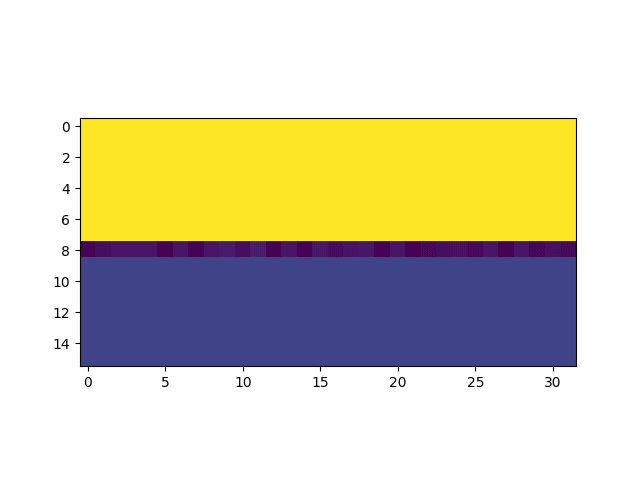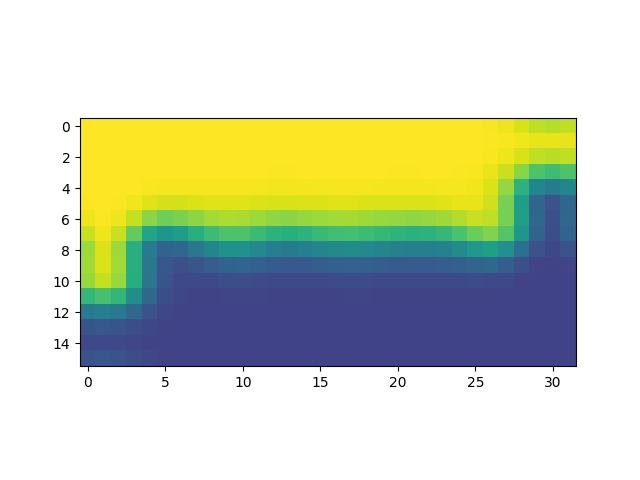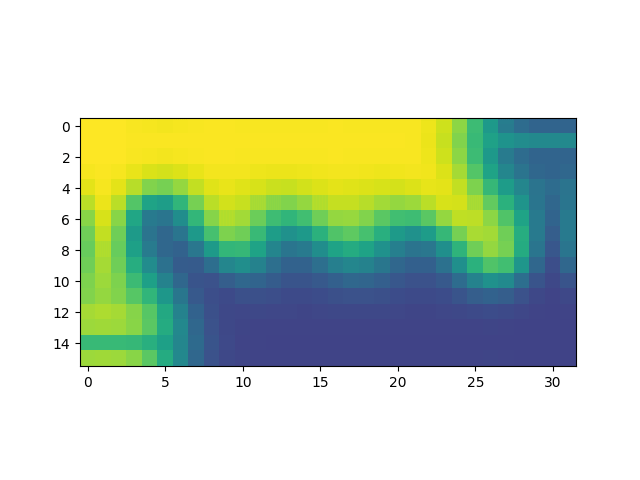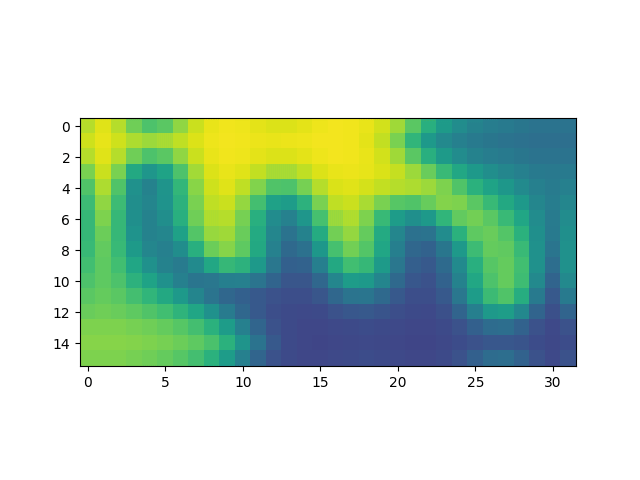
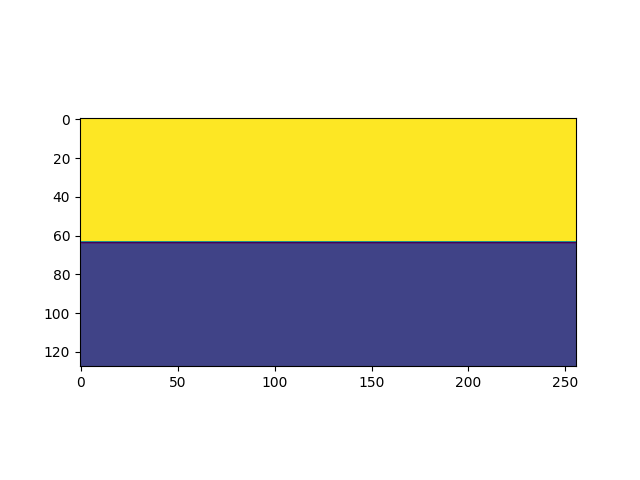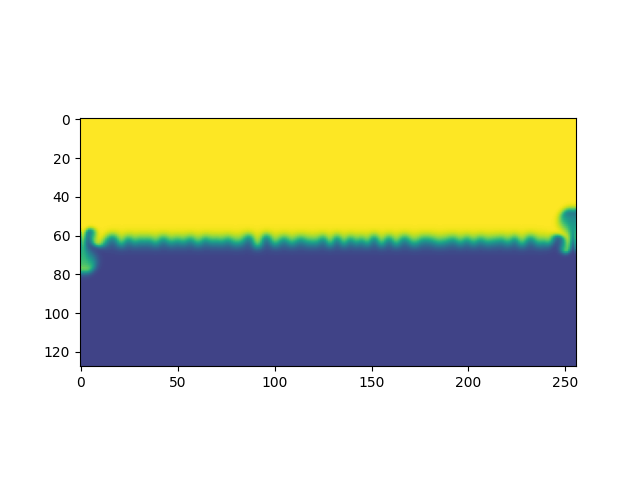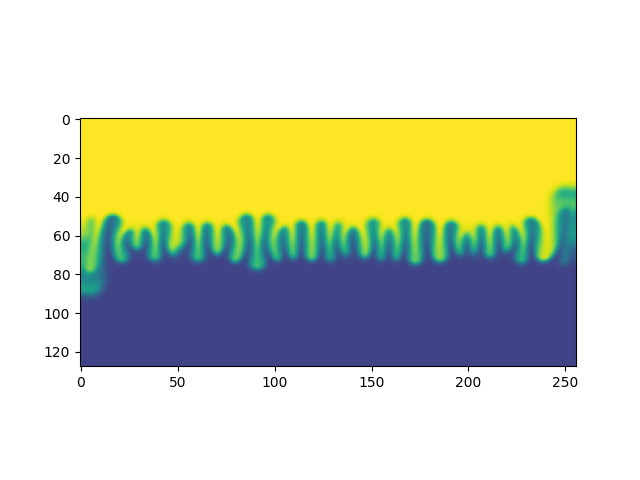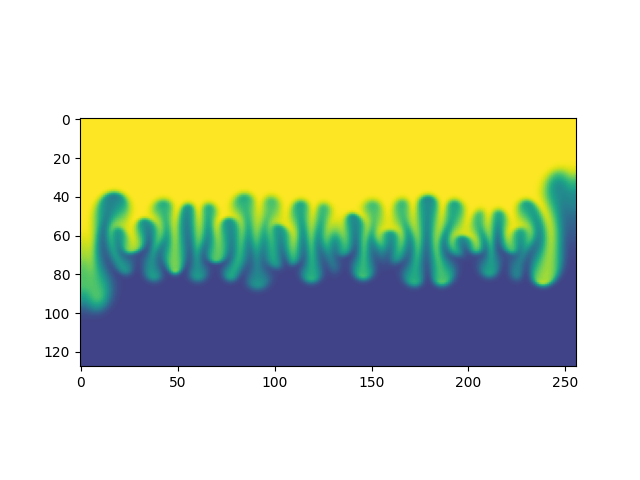
Duración en segundos de simulaciones de 100 pasos en grillas de distintos tamaños. Para cada tamaño de grilla se realizaron 20 simulaciones, excepto para la de tamaño 256 que se realizó una única simulación.

Utilizando un solver de sistemas lineales de Julia

Duración en segundos de simulaciones de 100 pasos en grillas de distintos tamaños. Para cada tamaño de grilla se realizaron 20 simulaciones, excepto para la de tamaño 256 que se realizó una única simulación.

¿Por qué necesito otro lenguaje de programación?

Important

Enfocandonos en el contexto de desarollo de Código para Cómputo Numérico y Científico

  • Procesamiento de grandes volumenes de datos
  • Resolución iterativa de algorítmos numéricos

Entonces surgen las preguntas

  • ¿Estoy usando el algoritmo de resolución correcto?
  • ¿Estoy usando las estructuras de datos correctas?
  • ¿Estoy manejando los recursos de la computadora de manera eficiente? (Memoria, CPU, GPU …)
  • ¿Cómo hago para responder las preguntas anteriores?
  • ¿Tengo las herramientas adecuadas para responderlas?
%%prun -s cumulative -q -l 20 -T prunX
n_pasos = 100
tamanio_grilla = 64 #128
simulacion(n_pasos,tamanio_grilla)

Con una grilla de tamaño 64

         4742152 function calls (4742143 primitive calls) in 6.555 seconds

   Ordered by: cumulative time
   List reduced from 196 to 20 due to restriction <20>

   ncalls  tottime  percall  cumtime  percall filename:lineno(function)
      2/1    0.000    0.000    6.554    6.554 {built-in method builtins.exec}
      2/1    0.000    0.000    6.554    6.554 <string>:1(<module>)
        1    0.000    0.000    6.554    6.554 <ipython-input-18-a8736b50808a>:1(simulacion)
      100    0.000    0.000    6.554    0.066 experimento.py:30(paso)
      100    0.001    0.000    6.554    0.066 simu.py:175(avanzar)
      100    0.001    0.000    6.540    0.065 simu.py:160(calcular_concentracion)
    56400    3.322    0.000    4.200    0.000 _basic.py:51(solve)
      100    0.021    0.000    3.319    0.033 simu.py:110(calcular_concentracion_x)
    18600    0.182    0.000    3.311    0.000 simu.py:122(calcular_columna)
      100    0.037    0.000    3.204    0.032 simu.py:79(calcular_concentracion_y)
    37800    0.323    0.000    3.166    0.000 simu.py:92(calcular_fila)
    56400    0.595    0.000    1.191    0.000 simu.py:153(construir_matriz_tridiagonal)
   112800    0.157    0.000    0.602    0.000 _util.py:275(_asarray_validated)
   169200    0.273    0.000    0.474    0.000 _twodim_base_impl.py:247(diag)
   112800    0.173    0.000    0.383    0.000 _function_base_impl.py:589(asarray_chkfinite)
    56401    0.050    0.000    0.271    0.000 fromnumeric.py:2349(sum)
   169201    0.267    0.000    0.267    0.000 {method 'reduce' of 'numpy.ufunc' objects}
    56400    0.200    0.000    0.232    0.000 simu.py:145(construir_coef_)
    56401    0.064    0.000    0.212    0.000 fromnumeric.py:69(_wrapreduction)
   112800    0.042    0.000    0.195    0.000 {method 'all' of 'numpy.ndarray' objects}

Con una grilla de tamaño 128

         9580953 function calls (9580911 primitive calls) in 47.932 seconds

   Ordered by: cumulative time
   List reduced from 232 to 20 due to restriction <20>

   ncalls  tottime  percall  cumtime  percall filename:lineno(function)
      2/1    0.000    0.000   47.932   47.932 {built-in method builtins.exec}
      2/1    0.001    0.000   47.932   47.932 <string>:1(<module>)
        1    0.011    0.011   47.931   47.931 <ipython-input-18-a8736b50808a>:1(simulacion)
      100    0.000    0.000   47.920    0.479 experimento.py:30(paso)
      100    0.001    0.000   47.920    0.479 simu.py:175(avanzar)
      100    0.003    0.000   47.874    0.479 simu.py:160(calcular_concentracion)
      100    2.158    0.022   32.653    0.327 simu.py:110(calcular_concentracion_x)
    37800    0.561    0.000   31.360    0.001 simu.py:122(calcular_columna)
   114000   21.674    0.000   24.122    0.000 _basic.py:51(solve)
   114000    8.781    0.000   18.364    0.000 simu.py:153(construir_matriz_tridiagonal)
      100    0.126    0.001   14.230    0.142 simu.py:79(calcular_concentracion_y)
    76200    0.825    0.000   14.135    0.000 simu.py:92(calcular_fila)
   342000    6.021    0.000    9.261    0.000 _twodim_base_impl.py:247(diag)
   570501    3.251    0.000    3.251    0.000 {built-in method numpy.zeros}
   228000    0.402    0.000    1.793    0.000 _util.py:275(_asarray_validated)
   228000    0.719    0.000    1.252    0.000 _function_base_impl.py:589(asarray_chkfinite)
       11    0.068    0.006    0.973    0.088 base_events.py:1909(_run_once)
   342001    0.811    0.000    0.811    0.000 {method 'reduce' of 'numpy.ufunc' objects}
   114001    0.133    0.000    0.810    0.000 fromnumeric.py:2349(sum)
   114001    0.162    0.000    0.655    0.000 fromnumeric.py:69(_wrapreduction)

Interoperabilidad con Julia

¿Por qué Julia Lang?

Queremos un lenguaje que sea de codigo abierto, con una licencia liberal.

Queremos la velocidad de C con el dinamismo de Ruby.

Queremos un lenguaje que sea homoiconico,

Queremos un lenguaje que sea homoicónico, con macros verdaderos como Lisp, pero con la familiar notación matemática como Matlab

Queremos que sea utilizable para programación general como Python, tan facil para la estadística como R, tan natural para procesamiento de texto como Perl, tan poderoso para algebra lineal como Matlab, tan bueno en unir programas como la shell.

Algo que sea muy simple para aprender, pero que deje feliz a los hackers más solemnes

Lo queremos interactivo y lo queremos compilado.

Why we created Julia

Mini demo de Julia

> julia

Llamar a Julia desde Python

Usamos el paquete juliacall

> python -m venv .venv
> ./.venv/bin/activate
> python -m pip install juliacall
from juliacall import Main as jl
s = r"""
using LinearAlgebra

function solve(A, b)
    A\b
end
"""

jl.seval(s)
solve_julia = jl.solve
from scipy.linalg import solve as solve_scipy
from numpy import array

A = array([[2,0,0],
           [0,2,-1],
           [0,-1,2]])
b = array([1,2,3])

solucion_scipy = solve_scipy(A,b)
solucion_julia = solve_julia(A,b)

SCA314

SCA314

Gracias!

Preguntas?

Los materiales de esta charla lo pueden encontrar en https://github.com/akielbowicz/pyday-catamarca-2024

Tip

Hay un par de diapos extras para que chusmeen

Más cosas para seguir aprendiendo

Cómo instalar Julia

La forma más práctica de instalar julia es usando el programa de la línea de comandos juliaup

En Linux:

> curl -fsSL https://install.julialang.org | sh

En Windows:

Es necesario scoop:

En una consola de PowerShell instalamos scoop con:

> Set-ExecutionPolicy -ExecutionPolicy RemoteSigned -Scope CurrentUser
> Invoke-RestMethod -Uri https://get.scoop.sh | Invoke-Expression

Y una vez instalado, instalamos juliaup

> scoop install main/juliaup

Y para empezar a desarrollar, lo más práctico es usar VSCode con la extensión de Julia

Materiales para aprender Julia

La documentación oficial docs.julialang.org

La página de Nothworthy Differences with Other Languages que describe las diferencias con otros lenguages como Python, Matlab, R.

Los Modern Julia Workflows

Hay un curso muy bueno del MIT sobre Parallel Computing and Scientific Machine Learning (SciML): Methods and Applications. Está super detallado y tiene las clases en YouTube.

El canal oficial de YouTube de @TheJuliaLanguage donde estan las charlas de las conferencias y meetups.

Características del lenguaje para seguir investigando

Introspección del Código

  • Benchmarking
  • Profiling
  • Code inspection

Features de Desarrollo

  • Multiple dispatch
  • Metaprogramación
  • Packaging y creación de Ambientes

Paquetes

Para buscar paquetes pueden usar el buscador en JuliaHub, algo similar a pypi.org para Python

Comunidades